声音合成的秘密『1』(声音中的秘密?)
声音合成的秘密『1』(声音中的秘密?)
在探索减法合成世界的第一章中,让我们返回到基础概念。什么是波形(waveforms)和谐波( harmonics),它们是怎么产生的,与我们所实际听到的声音相关理论又是怎样的?
抛开标题所说的不谈,我并不是要发表什么实际的真的秘密。但是在你没有耐心看完文章之前……我所做的是看一下声音合成、减法合成(这是很出名的法则,但是却又很难理解)的主要原则形式,以及这些法则又是如何被用于特定的合成器中。若你具有使用减法合成原理的合成器,且你知道如何在它上面得到你所想要的音色,但是你却不知道它们的工作原理,这些文章的目的便是或许能够填补一些你所不具备的空白知识(这不就是秘密吗,呵呵)。好的,我们或许应该起名叫合成器的如何如何之类的名字……但是,那却不是容易记住的名字,也不是全部的名字。那么首先的首先,什么是减法合成器?
“减法合成”一名来源于它所使用的方法,在“厚波”那里你减弱或移除去谐波以创造新的声音。你可使用静态模式来创造简单的音调,或者你也可以使用合成器中所提供的滤波器、波封发生器、调制器 来创造新的动感的令时间停止的声音,但是……你或许已经迷失了。到底什么是谐波?什么是波形?它们是怎么来的?在这个月里,我们直接面对这些概念,回答这三个问题。关于VCFs, EGs和 LFOs将在以后登出。
It's All Greek To Me
回答这个基本问题,我们必须跳到声音叠加机器时代(它或许正藏在某个复印机的下面,呵呵),来回顾一下有点模糊的过去。它在物理建模,采样器,模拟合成甚至是monosynths之前……
实际上,此处我们已处于严肃的专业领域,因为我们得返回到2500年前,来了解一下一个爱奥尼亚人叫 Pythagoras的家伙。Pythagoras或许是世界上第一个纯粹的数学家,当然我们对他的相关了解甚少(我们对他的了解无非就是一些传奇故事)。
归因于Pythagoras不被人知的发现之一是:扯动两根类似的同等紧度的细绳时会给发出令人愉悦的声音,若它们的长度都是整数相关(我的意思是可再进行分割的数字)。减法合成的名称就是从这个方法得来的,“经过从厚波中减弱或移除谐波来创造新的声音”。
例如,如果一根绳子一根绳子是其它一根的一半长度的话(1:2的关系),结果就会发出非常好听的声音。如果比例为2:3的话,声音听起来也不错。
不幸的是,Pythagoras及其后续人脱离了这个方向,并试图解释五个为人所知的行星及太阳和月亮的相似数字关系,这样便导致虚构的“music of the spheres”。如果他们把研究范围确定在那个小框里而不是如此大的领域(发现了Quantum Mechanics)的话,他们会有更大的成就。
但是Pythagoras strings的整数关系是为什么呢?若一根是另一根的1.21346706544倍又为何不发出令人愉悦的声音呢?
让我们扯动一下
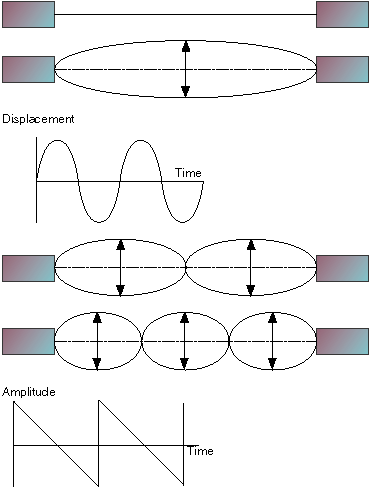
开始回答这个问题之前,让我们将一根细绳拉到所能承受的范围紧度,但又能震动的地步。如图一。
现在假设我们扯动绳子两端中间部分。正如你所想,这便是图二所示的震动。
这是“持续波”的一个例子。它并是象水波那样上下移动,但却上下震动。如果震动(vibration) (或者是oscillation)仅仅象图二所示,细绳中间的一个点简单移动的话,这个重复的模式叫正弦波(图三)。我们称呼这个模式为波形(waveform)震荡,这个在其单位时间内所做循环次数的频率就是绳子的基本频率(基频)。
这个基本模式并不是绳子震动的所有模式--尽管绳子两端是固定的。假设将你的手指放在绳子的正好中间(但是这样在整根绳子上仍然是震动的),扯动一边或者是另一边的话。你可以看到如图四所描述的静态波,如图四所示。
同样的,如果你在三分之一处尝试的话,会看到图五所示的震动,等等。
实际上,这些所谓的静态波在整根绳子上如图二所示的震动中都在发生,我们称这些波形为基频的谐波。
如果你学习静态波的数学原理的话,你会发现可将这种波形描述为两个运动方向相反的波形(不,你不要问为什么)。知道这个将会得出一个简单的结论:如果你等分波形长度,那么这个运动的频率会加倍。类似的,如果等分三部分,则三倍频率;四等分的话则四倍频率,以次类推……当然只对整数的分法应用,若你进行不是整数分法的话,细绳可能会不在零点上(我的意思是在一个循环周期内),这不可能的原因是因为两端被固定了。
无论如何,现在我们回答了所述的第一个问题,以及可通过一个简单的震荡器(oscillator)来确认谐波的方法:可震动模式。这个分析不是仅仅针对一根绳子。假设空气是立方体的空间。暂时忘记什么家具啦之类的,空气可以在任何地方震动除了墙面、地板。换句话说,震动就好象在一根绳子上一样。这就是为什么一般房子有共鸣的原因(resonances)--产生房间本身的谐波。这也是教堂风琴工作的原理--管子(pipes)实际上是个谐波震动器。
第一个谐波(基波:称为f)是扯动细绳时将会察觉的音调。第二个谐波(也被称为第一泛音)是一半基音波形长度所发的声音,频率增倍。孤立地看,我们察觉它们的形式为一个八度距离。
第三个谐波具备三倍频率(这是五度音),第四个谐波,具备四倍频率,又是基音的第二个八度。以此类推……
这就是我们要了解的Pythagoras原则。换句话说,因为那两根绳子的谐波结构类似,所以声音才会有愉悦感。
声音的性质
现在考虑如下:当你扯动一根绳子时,你不会听到单一谐波的声音。创造单一的状态为--在真实世界中--几乎为不可能,所以任何自然发出的声音实际上是很多不同数量谐波的组成。在任何时候,它都是如此,同时因为谐波数量的不同,波形可能比图三显示地要复杂的多。在一个对吉他声音或者是人声的编辑器中的波形分析中,你可以看到真实波形的复杂程度。
这样用来分析声音--或者是它的再合成--太难了,假如没有一个法国数学家傅立叶(Jean Baptiste Joseph Fourier)出现的话。这位同志的生活丰富多采,傅立叶依次做过教师,神秘的政治家,政治犯,埃及政府官员,Isère和Rh?ne的行政长官,同时还是拿破仑的好友。先不管这些,他发现不论是多么复杂的波形都可以由简单的谐波构成。这个原理就以其名称来命名。
坚持几秒钟……波形决定谐波,谐波决定波形?其实谐波和波形是以两种方法来解释一个事物的方式。这是个关键点:音色特性是由所含谐波的数量和振幅来决定的,任何给定的谐波也便给定了波形。所以当我们观察合成器上的震荡器时,或者说是诸如方波(square)或者是锯齿波(sawtooth),这其实是简单速记的方式,“这些设置产生特定的振幅X,振幅Y……的谐波”
减法合成
将这些注意用于合成器的话……看一下图六中的波形图。你决不可能从绳子上得到这种波形,但是你可以在几乎每一个合成器上找到近似的东东。这是一个锯齿波,以它的形状命名。
这种波形只带有一个简单的谐波关系,解释如下:
每一个谐波均存在,第N个谐波的振幅是基波的1/n。
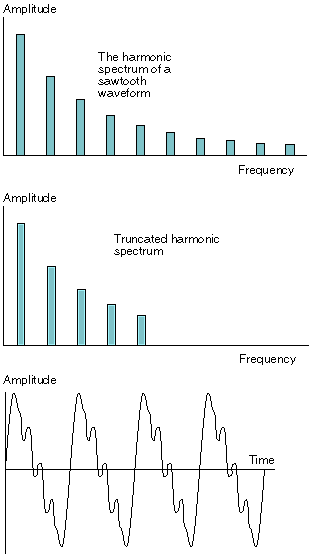
哦,这么说看起来不简单啊,但是相信我,其实远比这恶心得多。不管如何,看一下图7,它显示了开始的10个谐波, 你可以看一下它们的形状及频率。
但是若你修剪这些波形会如何呢?假设移除了除了前五个以外所有的谐波(得到这个结果你可以通过滤波器这个东东)。图8显示了频谱,图9显示了相对应的波形。
正如你所看到的,新的波形已同锯齿波不一样了,发出的声音也不一样了。但是唯一的不同是你修剪了锯齿波中的谐波。换句话说,你已经用滤波器“减去”了谐波,因此创造出新的声音效果。
那么便欢迎你来到减法合成的世界!!!!!!!!
在探索减法合成世界的第一章中,让我们返回到基础概念。什么是波形(waveforms)和谐波( harmonics),它们是怎么产生的,与我们所实际听到的声音相关理论又是怎样的?
抛开标题所说的不谈,我并不是要发表什么实际的真的秘密。但是在你没有耐心看完文章之前……我所做的是看一下声音合成、减法合成(这是很出名的法则,但是却又很难理解)的主要原则形式,以及这些法则又是如何被用于特定的合成器中。若你具有使用减法合成原理的合成器,且你知道如何在它上面得到你所想要的音色,但是你却不知道它们的工作原理,这些文章的目的便是或许能够填补一些你所不具备的空白知识(这不就是秘密吗,呵呵)。好的,我们或许应该起名叫合成器的如何如何之类的名字……但是,那却不是容易记住的名字,也不是全部的名字。那么首先的首先,什么是减法合成器?
“减法合成”一名来源于它所使用的方法,在“厚波”那里你减弱或移除去谐波以创造新的声音。你可使用静态模式来创造简单的音调,或者你也可以使用合成器中所提供的滤波器、波封发生器、调制器 来创造新的动感的令时间停止的声音,但是……你或许已经迷失了。到底什么是谐波?什么是波形?它们是怎么来的?在这个月里,我们直接面对这些概念,回答这三个问题。关于VCFs, EGs和 LFOs将在以后登出。

It's All Greek To Me
回答这个基本问题,我们必须跳到声音叠加机器时代(它或许正藏在某个复印机的下面,呵呵),来回顾一下有点模糊的过去。它在物理建模,采样器,模拟合成甚至是monosynths之前……
实际上,此处我们已处于严肃的专业领域,因为我们得返回到2500年前,来了解一下一个爱奥尼亚人叫 Pythagoras的家伙。Pythagoras或许是世界上第一个纯粹的数学家,当然我们对他的相关了解甚少(我们对他的了解无非就是一些传奇故事)。
归因于Pythagoras不被人知的发现之一是:扯动两根类似的同等紧度的细绳时会给发出令人愉悦的声音,若它们的长度都是整数相关(我的意思是可再进行分割的数字)。减法合成的名称就是从这个方法得来的,“经过从厚波中减弱或移除谐波来创造新的声音”。
例如,如果一根绳子一根绳子是其它一根的一半长度的话(1:2的关系),结果就会发出非常好听的声音。如果比例为2:3的话,声音听起来也不错。
不幸的是,Pythagoras及其后续人脱离了这个方向,并试图解释五个为人所知的行星及太阳和月亮的相似数字关系,这样便导致虚构的“music of the spheres”。如果他们把研究范围确定在那个小框里而不是如此大的领域(发现了Quantum Mechanics)的话,他们会有更大的成就。
但是Pythagoras strings的整数关系是为什么呢?若一根是另一根的1.21346706544倍又为何不发出令人愉悦的声音呢?
让我们扯动一下
开始回答这个问题之前,让我们将一根细绳拉到所能承受的范围紧度,但又能震动的地步。如图一。
现在假设我们扯动绳子两端中间部分。正如你所想,这便是图二所示的震动。
这是“持续波”的一个例子。它并是象水波那样上下移动,但却上下震动。如果震动(vibration) (或者是oscillation)仅仅象图二所示,细绳中间的一个点简单移动的话,这个重复的模式叫正弦波(图三)。我们称呼这个模式为波形(waveform)震荡,这个在其单位时间内所做循环次数的频率就是绳子的基本频率(基频)。
这个基本模式并不是绳子震动的所有模式--尽管绳子两端是固定的。假设将你的手指放在绳子的正好中间(但是这样在整根绳子上仍然是震动的),扯动一边或者是另一边的话。你可以看到如图四所描述的静态波,如图四所示。
同样的,如果你在三分之一处尝试的话,会看到图五所示的震动,等等。
实际上,这些所谓的静态波在整根绳子上如图二所示的震动中都在发生,我们称这些波形为基频的谐波。

如果你学习静态波的数学原理的话,你会发现可将这种波形描述为两个运动方向相反的波形(不,你不要问为什么)。知道这个将会得出一个简单的结论:如果你等分波形长度,那么这个运动的频率会加倍。类似的,如果等分三部分,则三倍频率;四等分的话则四倍频率,以次类推……当然只对整数的分法应用,若你进行不是整数分法的话,细绳可能会不在零点上(我的意思是在一个循环周期内),这不可能的原因是因为两端被固定了。
无论如何,现在我们回答了所述的第一个问题,以及可通过一个简单的震荡器(oscillator)来确认谐波的方法:可震动模式。这个分析不是仅仅针对一根绳子。假设空气是立方体的空间。暂时忘记什么家具啦之类的,空气可以在任何地方震动除了墙面、地板。换句话说,震动就好象在一根绳子上一样。这就是为什么一般房子有共鸣的原因(resonances)--产生房间本身的谐波。这也是教堂风琴工作的原理--管子(pipes)实际上是个谐波震动器。
第一个谐波(基波:称为f)是扯动细绳时将会察觉的音调。第二个谐波(也被称为第一泛音)是一半基音波形长度所发的声音,频率增倍。孤立地看,我们察觉它们的形式为一个八度距离。
第三个谐波具备三倍频率(这是五度音),第四个谐波,具备四倍频率,又是基音的第二个八度。以此类推……
这就是我们要了解的Pythagoras原则。换句话说,因为那两根绳子的谐波结构类似,所以声音才会有愉悦感。
声音的性质
现在考虑如下:当你扯动一根绳子时,你不会听到单一谐波的声音。创造单一的状态为--在真实世界中--几乎为不可能,所以任何自然发出的声音实际上是很多不同数量谐波的组成。在任何时候,它都是如此,同时因为谐波数量的不同,波形可能比图三显示地要复杂的多。在一个对吉他声音或者是人声的编辑器中的波形分析中,你可以看到真实波形的复杂程度。
这样用来分析声音--或者是它的再合成--太难了,假如没有一个法国数学家傅立叶(Jean Baptiste Joseph Fourier)出现的话。这位同志的生活丰富多采,傅立叶依次做过教师,神秘的政治家,政治犯,埃及政府官员,Isère和Rh?ne的行政长官,同时还是拿破仑的好友。先不管这些,他发现不论是多么复杂的波形都可以由简单的谐波构成。这个原理就以其名称来命名。
坚持几秒钟……波形决定谐波,谐波决定波形?其实谐波和波形是以两种方法来解释一个事物的方式。这是个关键点:音色特性是由所含谐波的数量和振幅来决定的,任何给定的谐波也便给定了波形。所以当我们观察合成器上的震荡器时,或者说是诸如方波(square)或者是锯齿波(sawtooth),这其实是简单速记的方式,“这些设置产生特定的振幅X,振幅Y……的谐波”
减法合成
将这些注意用于合成器的话……看一下图六中的波形图。你决不可能从绳子上得到这种波形,但是你可以在几乎每一个合成器上找到近似的东东。这是一个锯齿波,以它的形状命名。
这种波形只带有一个简单的谐波关系,解释如下:
每一个谐波均存在,第N个谐波的振幅是基波的1/n。
哦,这么说看起来不简单啊,但是相信我,其实远比这恶心得多。不管如何,看一下图7,它显示了开始的10个谐波, 你可以看一下它们的形状及频率。
但是若你修剪这些波形会如何呢?假设移除了除了前五个以外所有的谐波(得到这个结果你可以通过滤波器这个东东)。图8显示了频谱,图9显示了相对应的波形。
正如你所看到的,新的波形已同锯齿波不一样了,发出的声音也不一样了。但是唯一的不同是你修剪了锯齿波中的谐波。换句话说,你已经用滤波器“减去”了谐波,因此创造出新的声音效果。
那么便欢迎你来到减法合成的世界!!!!!!!!
文章出处 MIDI爱好者
转载文章请注明出自 Midifan.com
-
2018-10-24
 匿名
https://www.soundonsound.com/techniques/whats-sound
匿名
https://www.soundonsound.com/techniques/whats-sound -
2018-10-24
 匿名
原文链接: https://zh.scribd.com/document/159566823/Synth-Secrets-Part-1-What-s-in-a-Sound
匿名
原文链接: https://zh.scribd.com/document/159566823/Synth-Secrets-Part-1-What-s-in-a-Sound -
2016-08-17
 匿名
能不能给个原文链接?翻译得太影响理解了,想看看原文
匿名
能不能给个原文链接?翻译得太影响理解了,想看看原文 -
2016-07-03
 匿名
内容不错。但感觉作者表达能力有问题
匿名
内容不错。但感觉作者表达能力有问题 -
2012-03-12
 鹤峰
深奥
鹤峰
深奥 -
2012-03-12
 鹤峰
哈哈,初学,难懂
鹤峰
哈哈,初学,难懂




